机器学习 | 线性模型之Logistic回归

对数几率回归：（Logistic回归）

解决二分类问题
<div align=center>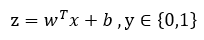</div>
 

单位阶跃函数：(不连续、理想状态)
<div align=center>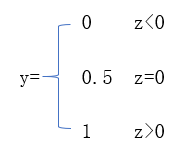</div>
<div align=center>y代表输出标记，z代表预测值</div>

预测值大于零就判为正例，小于零就判为反例，预测值为临界值零则可任意判别

对数几率函数（可微、任意阶可导）（替代函数）

<div align=center>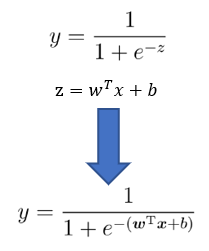</div>
 

对数几率（log odds）：本作为正例的相对可能性的对数

<div align=center>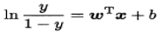</div>
 

单位阶跃函数与对数几率函数的比较

<div align=center>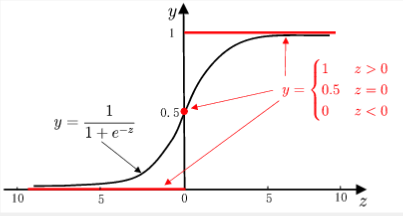</div>
 

对数几率回归优点

1. 无需事先假设数据分布
2. 可得到“类别”的近似概率预测
3. 可直接应用现有数值优化算法求取最优解

对数几率（log odds）

<div align=center>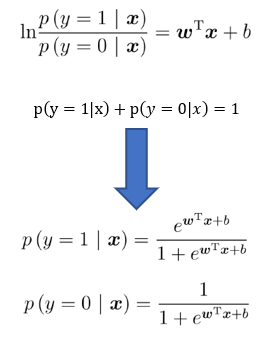</div>
 
 

极大似然法

给定数据集：
<div align=center>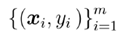</div>

最大化样本属于其真实标记的概率：（连乘容易下溢）
<div align=center>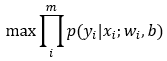</div>
 

最大化对数似然函数：令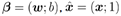
<div align=center>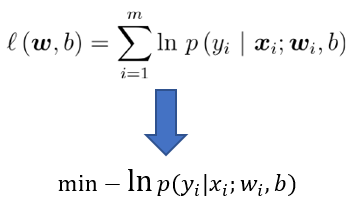</div>
 
<div align=center>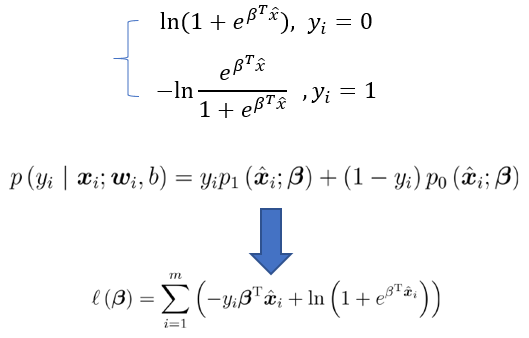</div>
 

高阶可导连续凸函数，梯度下降法/牛顿法求其最优解：.
<div align=center>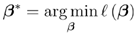</div>
 
 

梯度下降法

<div align=center>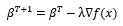</div>
 
 

牛顿法：（第t+1轮迭代解的更新公式）

<div align=center>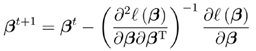</div>
 

其实就是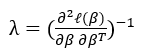 的梯度下降法
 

其中关于β的一阶、二阶导数分别为
<div align=center>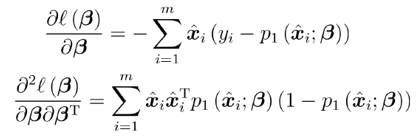</div>